EKF and ESEKF
1. EKF(线性化卡尔曼滤波)
当运动和观测方程不是线性的情况下。为了简化计算,使用一阶泰勒分解线性化运动方程和观测方程。
对于EKF,采用上一个最优状态估计进行线性化
线性化模型方程
\[x_k = f_{k-1}(x_{k-1}, u{k-1}, w_{k-1})\approx f_{k-1}(\hat x_{k-1}, u_{k-1}, 0) + \left.\frac{\partial{f_{k-1}}}{\partial{x_{k-1}}}\right|_{\hat x_{k-1}. u_{k-1}, 0}(x_{k-1}-\hat x_{k-1}) + \left.\frac{\partial{f_{k-1}}}{\partial{w_{k-1}}}\right|_{\hat x_{k-1}. u_{k-1}, 0}w_{k-1}\]线性化观测方程
\[y_k = h_k(x_k, v_k)\approx h_k(\breve x, 0) + \left.\frac{\partial{h_k}}{x_k} \right|_{\breve x, 0}(x_k - \breve x_k) + \left.\frac{h_k}{v_k}\right|_{\breve x_k, 0}v_k\]EKF存在的问题
运动及观察模型用泰勒级数的一阶或二阶展开近似成线性模型,忽略了高阶项,不可避免的引入线性误差,甚至导致滤波器发散
总结
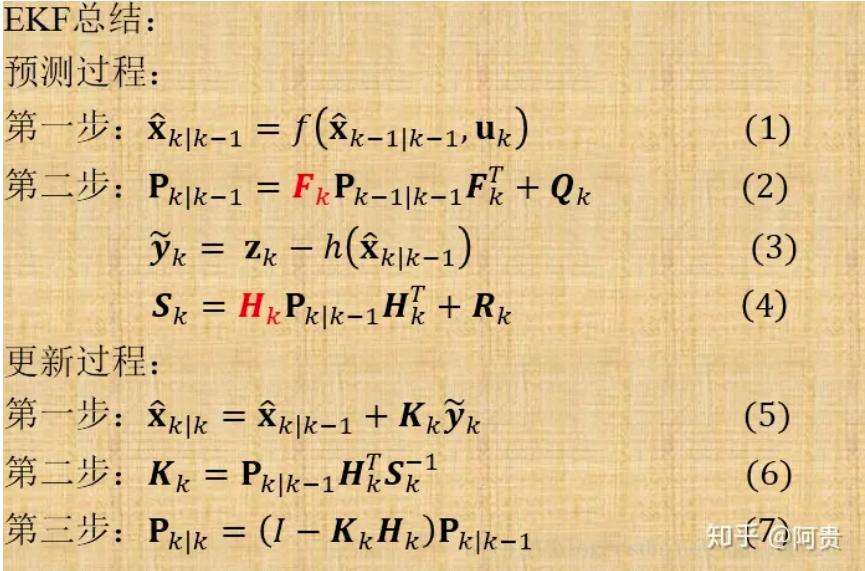
拓展
迭代卡尔曼滤波器

2. ESEKF(误差状态拓展卡尔曼)
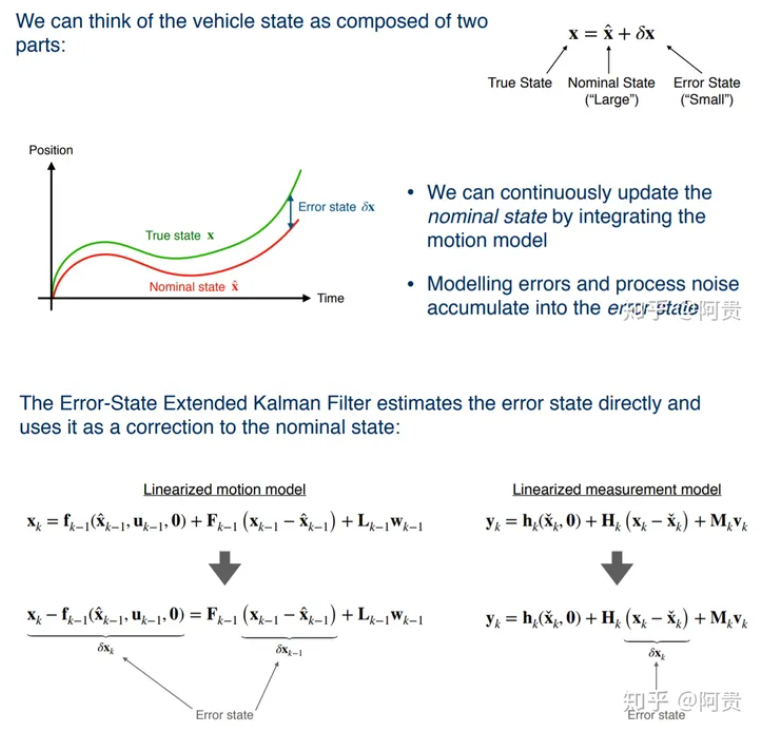
更新步骤
- Update norminal state with motion model
利用上一时刻的状态和当前输入,更新当前时刻的状态先验 \(\breve x_k = f_{k-1}(x_{k-1}, u_{k-1}, 0)\)
- Propagete uncertainty
利用上一时刻的方差矩阵后验,更新得到当前的方差先验 \(\breve P_k = F_{k-1}P_{k-1}F_{k-1}^T + L_{k-1}Q_{k-1}L_{k-1}^T\)
-
if a measurement is available, compute Kalman Gain \(K_k = \breve P_kH_k^T(H_k\breve P_kH_K^T)^-1\)
-
compute error state \(\delta\hat x_k = K_k(y_k - h_k(\breve x_k, 0))\)
-
Correct norminal state
- Correct state covariance
为什么说ESEKF相比于EKF有更好的效果呢
1.由于相比于原有的状态,误差这个状态量更小,并且非线性程度不高,线性化带来的误差更少。详细见下图,ESEKF在名义状态处线性化的非线性程度相比于EKF更小。原因,$F(t) = \frac{\partial f}{\partial\breve x}$ 与误差状态无关,因此ESKF的System Model是一个线性时变系统。其线性化程度比EKF要好很多。
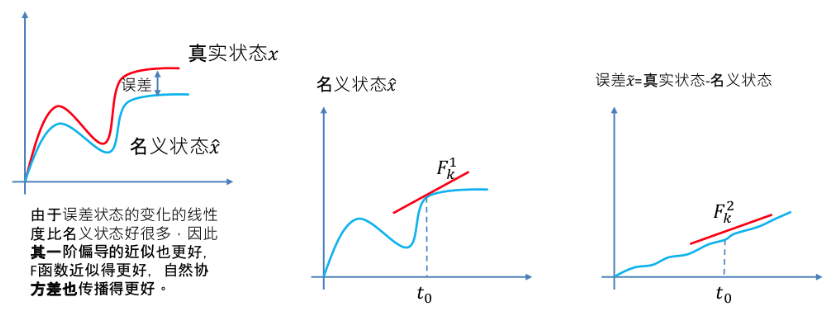
2.ESKF的状态量更好优化,更容易在限制的条件下工作,例如3D空间下的旋转
$x = \hat x\oplus\delta x$,其中$\hat x$是名义模型,是超参数的带有限制的。例如需要模为1的四元素。而$\delta x$是最小参数化的,是不带限制的。
在EKF中,如果一个旋转量表示为欧拉角,三个参数三个自由度,那么在优化的过程中可能会出现万向节死锁的情况。如果表示为四元素,那四个参数表示三个自由度,并且需要满足模为1的约束,那在优化的时候可能会出现协方差奇异的情况。
但是在ESEKF中,一个误差量表示为欧拉角的过程中,由于误差状态是个小量,不用担心万向死锁的情况。当表示为四元素的时候,可以将名义模型作为带限制的参数,优化模型的w设置为1,只要优化三个参数。