欧式聚类,K-maens,DBSCSN,mean-shift算法原理
欧式聚类
KD-Tree
KD-Tree是将数据点在K维空间中划分的一种数据结构,是一种平衡二叉搜索树。KD-Tree是每个节点均为k维数值点的二叉树,其上的每个节点代表一个超平面,该超平面垂直于当前划分维度的坐标轴,并在该维度上将空间划分为两部分,一部分在其左子树,另一部分在其右子树。即若当前节点的划分维度为d,其左子树上所有点在d维的坐标值均小于当前值,右子树上所有点在d维的坐标值均大于等于当前值,本定义对其任意子节点均成立。
KD-Tree构建方法:
- 对于n维的数据集,首先寻找方差最大的那个维度,然后将找到这个维度的中位数,将数据集一分为二。
- 对数据集递归地进行划分,直到不能够划分为止
KD-Tree最近邻搜索算法:
- 首先按照非叶子节点中的分割维度和中位数,直到搜索到叶子节点。
- 遍历到叶子结点后,回溯到当前节点的父节点,如果没有更小的点,那就再往上,直到回溯到根节点
欧式聚类原理
找到空间中的某一个点,利用kd-tree找到离他最近的n个点,判断这n个点的聚类,将距离较近的点放入集合中。重复上一步骤,直到集合里面没有新的元素能够加入。

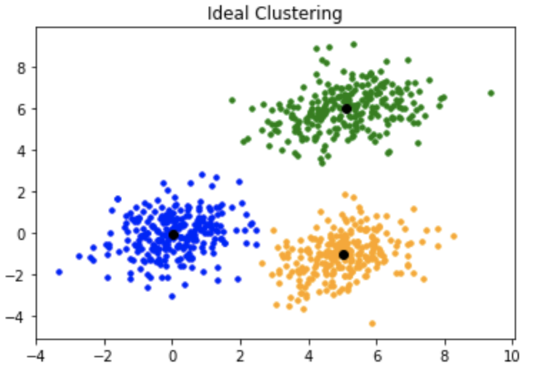
K-means算法
首先输入K个聚类簇和终止迭代的阈值,输出是聚类分割的结果。
- 首先初始化K个聚类簇中心,计算每个数据对象到聚类簇的距离,然后将数据对象划分聚类,并计算距离和J1。
- 将所得的聚类计算聚类簇中心,同时计算新的距离和J2。
- 计算$\Delta J$。判断\Delta J$是否小于阈值或者大于迭代次数,如果是则跳出循环。
- 根据所得的聚类簇,得到新的聚类中心,计算新的距离J1。
K-means算法优缺点
- 算法简单
- 需要实现指定聚类簇的个数
- 对异常点敏感
- 容易陷入局部最优
- 只能发现球形聚类簇
DBSCAN密度聚类
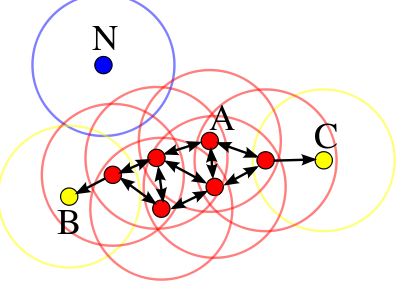
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,是一种具有噪声的基于密度的聚类方法。
DBSCAN中簇的定义是密度相连的点的最大的集合,就是将足够高密度的区域划分为簇,并可以仍受一部分噪声点。
算法利用一组邻域来描述样本集的紧密程度,参数$(\epsilon, MinPts)$来表述邻域样本的紧密程度。$MinPts$表示的是以半径为$\epsilon$的领域中数据点的最小个数。
核心对象:如果一个点周围领域内有超过$MinPts$的点,那么他是核心对象。
密度直达: 核心样本周围的点都是密度直达的
密度可达: 核心对象之间可以传递密度直达的对象。a点是b点的密度直达,b点和c点是互为核心对象,那么a点对于c点也是密度直达。
密度相连: 两个点可以通过一系列的核心点相连,那么就是密度相连。
算法流程
- 输入样本集$D = {x_1, x_2 ,…, x_m}$,领域参数$(\epsilon, MinPts)$。初始化核心对象集合和类别
- 遍历集合D,如果是核心对象,则将其加入到核心对象集合
- 如果核心对象集合内的元素都被访问,算法结束,否则转入步骤4
- 在核心对象集合中,随机选择一个未访问的核心对象,标记为已访问,记录类别为k。将其领域中未访问的数据加入种子点集合Seeds中。
- 如果种子点集合$Seeds=\varnothing$,则当前聚类簇生成完毕,k=k+1,跳转3。否则,从种子集合Seeds中挑选一个种子点seed,首先将其标记为已访问,标记类别为K,然后判断seed是否为核心对象,如果是将seed中未访问的种子点加入到种子集合中,跳转到5。
算法优缺点
- 如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合。
- 如果样本集较大时,聚类收敛时间较长
- 调参相对于传统的K-Means之类的聚类算法稍复杂,主要需要对距离阈值ϵ,邻域样本数阈值MinPts联合调参,不同的参数组合对最后的聚类效果有较大影响。
Mean Shift聚类算法
简单的来说就是将聚类里面的点看做是各自方向的力,通过计算每个点的合力,然后将圆心的位置漂移
算法流程
OPTICS聚类算法
核心距离: 使得一个点成为核心点的最小邻域半径
可达距离: x成为核心点,y可以从x直接密度可达成立的最小邻域半径
OPTICS算法是DBSCAN算法的改进版本,由于DBSCAN算法对输入参数$(\epsilon, MinPts)$过于敏感,所以OPTICS对算法中的$\epsilon$固定为无穷大,同时并不显式生成数据聚类。
算法思想: